Better Odds: Outside the Box
Being creative with strategy is different from directing creativity with strategy.
So, we’ve talked about how colour-by-numbers strategy leads to pointier questions, which lead to better ideas. We’ve talked about how new information and questioning unquestioned assumptions can provide one kind of insight, which can lead to even better ideas. And most recently, we’ve talked about uncertainty around the quality of ideas and how to evaluate them with varying levels of confidence.
We’ve also got a picture of what’s happening to the distribution of idea quality when we use colour-by-numbers strategy to narrow down to pointier questions:
That is, the average quality increases (the peak shifts to the right) and the curve bunches up. (Technically, this bunching is a drop in the standard deviation.)
And with the NZ Blood case study as an example, we’ve got a picture of what happens when we use new data to focus down to even more relevant issues, which we weren’t aware of previously:
That is, the peak shifts further to the right than was possible with the previous information. A new level of quality (typically effectiveness) in ideas is made possible.
When I look at these kinds of situations, I feel very comfortable with the strategy and confident in the relative superiority of the ideas that come from it. Colour-by-numbers strategy is very reliable. If you focus your attention on the most influential and influenceable factors in a challenge, you simply will, on average, have more effective ideas. By the same logic, if you uncover new information which reveals an even more influential and influenceable factor, then ideas from focusing on it will be even more effective again.
The merits of each idea relative to each other might be uncertain and require some validation or testing, but you’ll be choosing between ideas that are, on average, more effective than they would have been without strategic thinking. The quality of these questions is predictable.
But there are some kinds of questions to prompt ideas where the quality of the questions is more uncertain. These are questions where you don’t know how good the ideas will be until you start having them.
Now, you might ask, why on earth would we want questions of uncertain quality when we can use colour-by-numbers strategy to arrive at pointier questions which will certainly produce better ideas? The answer goes back to our discussion of horizons of disclosure and obviousness.
Basically, colour-by-numbers strategy and its pointier questions all take place within the most obvious, available mental model for understanding the situation and the challenge. This mental model, the box we’re thinking inside of, comes with a floor and a ceiling of the quality of ideas we can have. New information, like in the NZ Blood case, can raise that ceiling. But while it can seem like there’s a lot of variety in how good or bad the ideas can be, it’s actually a relatively narrow range compared to what is really possible.
To illustrate this with an analogy, consider the high jump in athletics. Prior to 1968, the dominant high-jump technique was called the “straddle”, because the athlete would throw one leg across and follow it with the other – straddling the pole. Some people were better or worse at this technique, and the best won gold medals. Following colour-by-numbers strategy, no doubt some coaches and athletes came up with new ideas of how to improve their straddle technique, new exercises to improve their form, etc. To improve their high jump success, they came up with ideas to improve their straddle technique.
Then Dick Fosbury came along and did this:
He flung his whole body, back first, over the pole. This technique became known as the Fosbury Flop. And athletes using it would, on average, outperform athletes using the straddle technique. So, of course, all athletes dropped the straddle technique and adopted the Fosbury Flop (it became the new best practice) and some were better or worse than each other.
Coming up with the Fosbury Flop was impossible to someone whose understanding of the high-jump challenge was “how to improve the straddle technique the most”. It’s worth noting that the Fosbury Flop wasn’t actually viable until shortly before Dick’s gold medals. New deep foam pads meant he could land like that safely. In other words, it was a trend in technology that made the new technique possible, but his competitors were too fixed on the obvious (straddle) mental model to see the possibilities the new technology opened up.
So what I’m suggesting is twofold – firstly, that there are non-obvious questions that can produce much better (and worse) ideas than the more obvious ones; and secondly, that we often can’t tell in advance how good or bad these questions will be at prompting effective ideas.
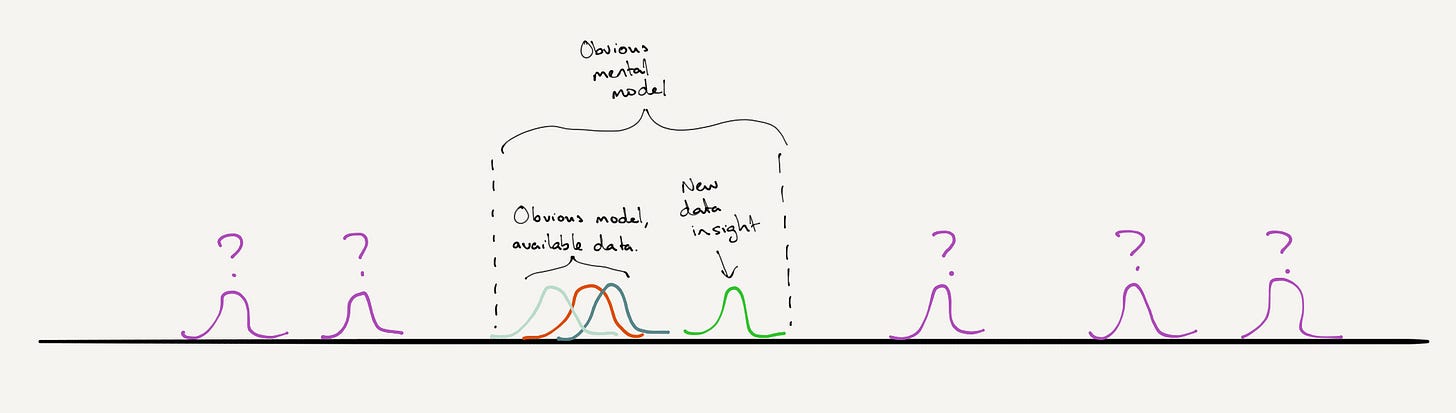
Excuse the sketching, but it would take me too long to make this look prettier in Excel:
The words are a bit small for reading, but what we have here is…
Our familiar cluster of better or worse questions within the most available mental model using the available data.
Our better question and ideas from the new data insight, still within the same mental model for understanding the challenge.
A bunch of possible questions, of uncertain quality, outside of the obvious ways of thinking about the challenge. (Those are question marks above them.)
It should be clear why we would consider stepping outside of our familiar and reliable colour-by-numbers approach. Unless we do, big step changes in idea quality are not possible. But if we do, much worse ideas also become possible. (Wasting time, if nothing else.) The real question is – without the confidence we get from colour-by-numbers strategy, how do we know which question to ask? Which out-of-the-box ideation prompt do we use?
This is exploratory thinking. As I said earlier, with these kinds of questions, we can’t know how good the ideas will be until we try coming up with those ideas off that question. If we pick one, we are basically rolling the dice and hoping the approach will be superior to the obvious way of seeing things and the ideas that would be prompted within that obvious mental model.
So you don’t pick just one. Let’s say you pick ten different ideation prompts, ten different questions to be answered, which have come from stepping outside the obvious and usual way of thinking about the problem. You’re spreading your efforts across more approaches. Some of the prompts will be better than others. One might produce great ideas.
What does that distribution of idea quality look like on our chart?
Well, this is a bit stylised, but it looks like this:
That is to say, it’s a flatter curve. It is, in fact, the opposite of what we achieve by focusing down to pointier questions. And here, finally, is the answer to the question I asked weeks ago. If the goal is to increase the number of great ideas, and great ideas are on the far right of this distribution curve, then a flatter curve will mean more great idea. More great ideas, more terrible ideas, fewer average ideas. And this comes from having a number of questions of uncertain quality.
To me, this is a very important aspect of strategy, creativity, and effective action. We have two broad ways of approaching a challenge:
Use colour-by-numbers strategy to develop a pointier question which incrementally increases idea quality with high confidence, but makes exponentially better ideas impossible. This looks like a bunching up of the distribution curve and an improvement in average quality.
Break out of the obvious to develop a range of exploratory questions which make exponentially better ideas possible, but also burn time coming up with terrible ideas, and with much lower confidence in the outcomes. This looks like a flattening of the distribution curve and no improvement in average quality.
The two aren’t entirely mutually exclusive. Whenever I’m running an ideation workshop, I lead up to the ideation exercises with activities that generate both reliable pointy prompts (colour-by-numbers) and unreliable wildcard prompts (non-obvious approaches). This leaves me reassured of a high chance of good ideas (from the pointy prompts) while also leaving the door at least open to great ideas (from the non-obvious prompts).
But generally, when should you use each approach to strategy? Well, I’ll come back several times to different applications of this trade-off, but the short answer is:
If you need a good idea in a hurry, use colour-by-numbers strategy to generate the best few pointy questions you can.
If you need a great idea and have time to explore, use non-obvious strategy to generate a range of exploratory questions.
Finally, again, stakes are relevant. You don’t need a great idea for Wednesday morning’s Facebook post. A good idea will do. But if you’re looking for ways to outcompete in a highly commoditised market that’s dominated by a few big competitors, merely good ideas won’t be good enough and the returns on a great idea could be huge.